共通部分 (数学)

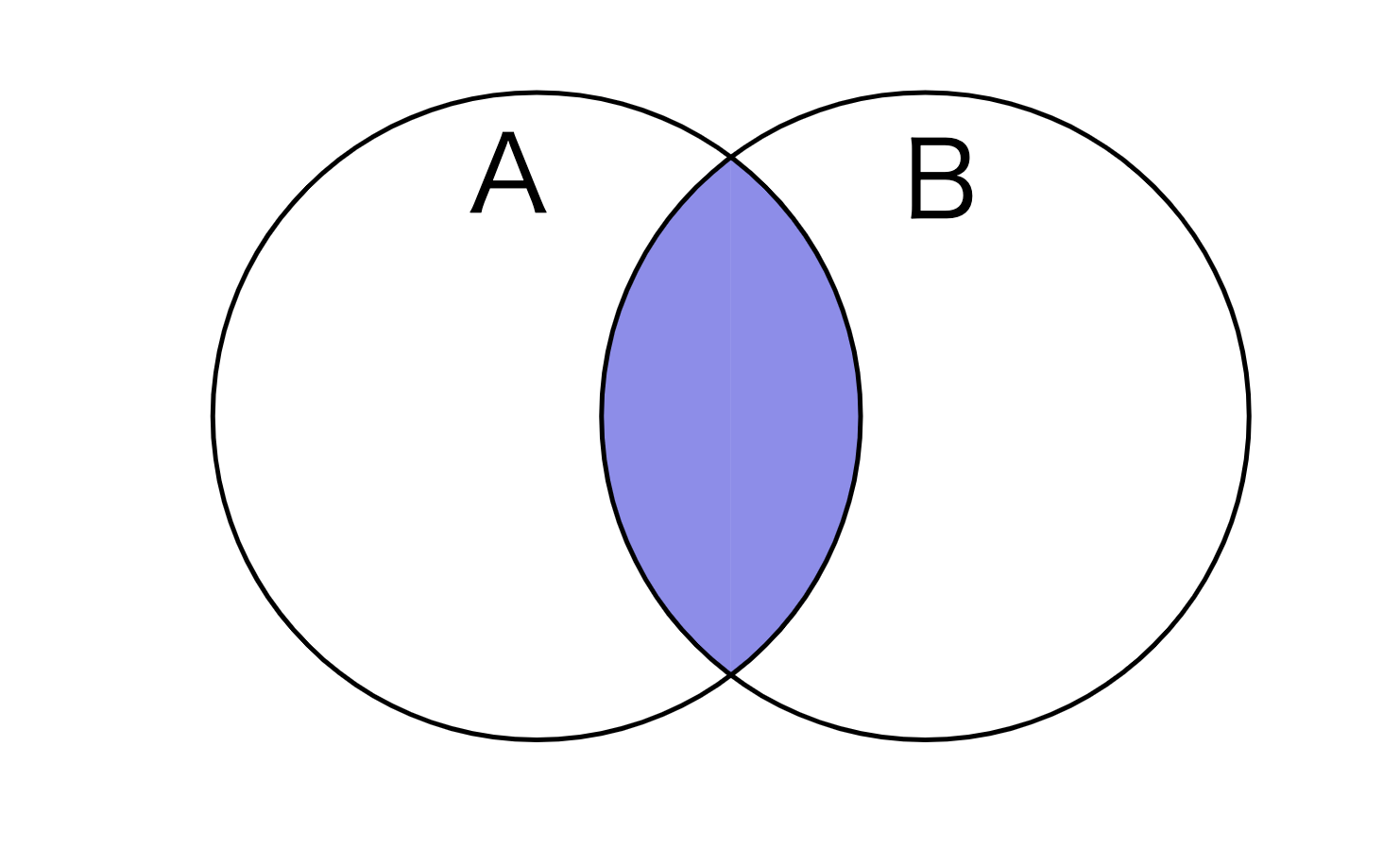
数学において、集合族の共通部分（きょうつうぶぶん、英: intersection, meet）とは、与えられた集合の集まり（族）全てに共通に含まれる元を全て含み、それ以外の元は含まない集合のことである。

共通集合（きょうつうしゅうごう）、共通分（きょうつうぶん）、交叉（こうさ）、交差（こうさ）、交わり（まじわり）、積集合（せきしゅうごう）、積（せき）などとも呼ばれる。

ただし、積集合は直積集合の意味で用いられることが多い。

定義

二つの集合の交叉

集合 A, B の交わりは A ∩ B と記される。これは

x ∈ A ∩ B ⇔ x ∈ A かつ x ∈ B

ということであり、記号では

A ∩ B = { x | x ∈ A ∧ x ∈ B }

と書ける。A ∩ B に含まれるような元が存在するとき A と B とは互いに交わるあるいは交わりを持つという。

また、そのような元の存在しないとき A と B は互いに素であるまたは交わりを持たない (disjoint) といい、

A ∩ B = ∅

と書く。ただしここで、 ∅ は空集合を表す。

有限個の交叉

有限個の集合 M₁, … M_k の交わり

M_{1}\cap M_{2}\cap \cdots \cap M_{k}

は、そのすべてに共通に含まれる元の全体である。集合の交わりは結合的、つまり

(A ∩ B) ∩ C = A ∩ (B ∩ C)

を満たすから、（一般結合法則）により有限個の集合の交わりは

(\cdots ((M_{1}\cap M_{2})\cap M_{3})\cap \dotsb \cap M_{k})

に等しく、また括弧の付け方に依らない。

\bigcap _{n=1}^{k}M_{n}=M_{1}\cap M_{2}\cap \dotsb \cap M_{k}

とも表す。

任意の交叉

集合の（空でない）族

{\mathfrak {M}}=\{M_{\lambda }\}_{\lambda \in \Lambda }

に対して、その交わりを集合族に属する全ての集合に属する元、つまり

すべての λ ∈ Λ に対して x ∈ M_λ

となる x の全体であると定義して

\bigcap {\mathfrak {M}},\quad \bigcap _{M\in {\mathfrak {M}}}M,\quad \bigcap _{\lambda \in \Lambda }M_{\lambda }

などで表す。特に集合列 {M_n}_n∈N の交わり（可算交叉）の場合には

\bigcap _{n=1}^{\infty }M_{n}=M_{1}\cap M_{2}\cap M_{3}\cdots =M_{1}\cap (M_{2}\cap (M_{3}\cap \cdots ))

のようにも書く。

与えられた集合族の共通部分が空集合となるとき、つまり全ての集合に共通に含まれる元が一つも存在しないとき、その集合族は交わりを持たない (disjoint) という。また、どの二つの集合を取っても交わらないとき、その集合族は対ごとに交わりを持たない (pairwise disjoint) と言う。disjoint ではないが pairwise disjoint な集合族が存在する。

例

P = {1, 3, 5, 7, 9} （10 以下の奇数の集合）、Q = {2, 3, 5, 7} （10 以下の素数の集合）とすると、P ∩ Q = {3, 5, 7} である。また、R = {2, 4, 6, 8, 10} （10 以下の偶数の集合）とすると P と R には共通の要素が存在しないから P ∩ R は空集合である。

実数からなる開区間の族 M = {(0, 1 1/n) | n は 1 以上の自然数} の共通部分は半開区間 (0, 1] である：

\bigcap \mathbf {M} =\bigcap _{n=1}^{\infty }\left(0,\,1 {\frac {1}{n}}\right)=(0,1].

実際、 (0, 1] はどの区間にも含まれるので共通部分に含まれることは直ちに言える。一方、1 < x とするならば x = 1 ε となる正の実数 ε が取れるが、1 / ε < n なる自然数は必ず存在して、x はそのような n に対する (0, 1 1 / n) に属さない。したがって上記の等式が成立する。また、同様の区間族 L = {(0, 1 − 1/n) | n は 1 以上の自然数} は n = 1 に対応する区間が空集合であるので共通部分 ∩ L も空集合、つまり L は交わりを持たない。

空なる交叉

上記、任意個数の集合の交叉の定義において、族が空集合 (∅) となる場合を排除したことに注意しなければならない。これは集合族 M の交わりを

\bigcap \mathbf {M} =\{x:\forall A\in \mathbf {M} ,\ x\in A\}

で定義するために、M が空ならば A ∈ M なる集合は存在しないから「x が満たすべき条件は一体何であるか」という問題を生じるからである。M が空なるときの上記条件は空虚な真の一例であるから、答えは「可能な限りの全ての x」となるべきである。すなわち、空な集合族の交わりは普遍集合（交叉演算の単位元）と定義することになる。

困ったことに標準的な集合論 (ZFC) には普遍集合が存在しないから、これを部分的に回避するために宇宙と呼ばれる一つの大きな集合 U を固定してその部分集合となる集合のみを考えることがよく行われる。このような条件下での U の部分集合族の交わりは