ラグランジュ点

ラグランジュ点（ラグランジてん、英語: Lagrange point あるいは Lagrangian point(s)）は、天体力学における円制限三体問題の5つの平衡解であり、二つの天体系から見て第三の天体が安定して滞在し得る位置座標点である。ラグランジュ点において第三の天体は、二つの天体から受ける重力と慣性力（遠心力）の釣り合いが取れており、外力による加速を受けない。5つすべての平衡解（座標点）を解析的に発見したジョゼフ＝ルイ・ラグランジュにちなんで命名されている。

ラグランジュ点は、巨大な質量をもつ二つの天体の系において、この二つの天体と比べてはるかに小さな質量の第三の天体についてもっぱら議論される。巨大な質量の二天体の例として、恒星-惑星の系（太陽-木星の系 (木星トロヤ群)、太陽-地球の系など）や惑星-衛星の系（土星-土星の衛星の系、地球-月の系など）があげられる。

概要

ある天体Eの周りを何らかの天体Mが回り、EとMのほかに天体がない場合、これらの天体の軌道を求めることは、力学における二体問題に相当する。この解は古典力学の最初期にアイザック・ニュートンによって見い出されており、天体Mの一般的な軌道は楕円軌道である。例えば、Eを地球、Mを月とすると、地球と月が互いの引力に束縛された系の比較的簡単な問題として扱うことができる。

しかし、さらにここに第三の天体Aがある場合には、各天体の軌道を求めることは二体問題に比べて遥かに難しくなる。天体E、天体Mおよび天体Aの3つについて、互いの重力の影響を受ける状況下でのそれぞれの軌道を求めることは、三体問題と呼ばれる問題の特別な場合にあたる。たとえば、前述の地球と月の系に第三の天体を加えた系の軌道の解析も三体問題である。一般の三体問題では解析解を得られないことが知られている。

ラグランジュ点を求める問題は、この三体問題の解のうち、第三の天体Aが他の二つの天体に比べて質量が無視できるほど小さいと仮定したとき、それが恒常的にいかなる力も受けない位置を求めることに相当する。1760年頃に、レオンハルト・オイラーがトロヤ点以外の3つのラグランジュ点を解析的に発見した（オイラーの直線解）。その後の1772年に、ジョゼフ＝ルイ・ラグランジュは論文『三体問題に関するエッセイ』において、オイラーの直線解は一般の三体問題の場合にも成り立つことを説明し、加えて、トロヤ点を含む5つすべてのラグランジュ点を求めることに成功した。ラグランジュ点を求めるにあたっては、一般に次の仮定をおく。

• 2つの天体EとMは、これらの重心を共通の中心とする円を軌道として回転運動している。
• 第三の天体Aの質量は、天体Eと天体Mの各質量に比べて、無視できるほど小さい。
• 天体Aは、天体Eと天体Mの公転軌道を含む平面上でのみ運動する。
• 天体Aの運動を考えるに際して、天体Eと天体Mが常に静止しているようにみえる回転座標系を採用する。すなわち、「天体Eと天体Mの重心を中心として、これらの公転周期に相当する角速度で回転する座標系」を採用する。
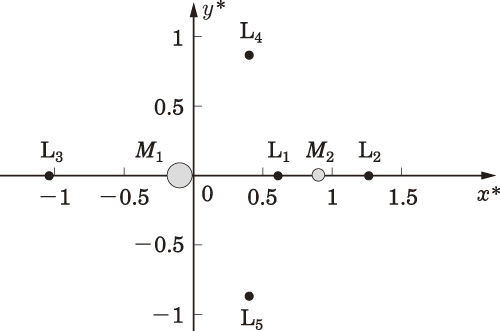
  • ここでもし、天体Eが天体Mより十分に大きな質量を有していれば、冒頭の図のように、回転座標系において天体Eが中心にあり、天体Mは公転軌道を示す円上の一点で静止している、とほぼ見做すことができる。

以上の仮定のもとで求めた、第三の天体Aが力を受けない座標位置がラグランジュ点である。天体Aはこの回転座標上のラグランジュ点において、安定に留まれる（すなわち、天体Eや天体Mに対する静止位置を保てる）可能性がある。天体Aはラグランジュ点において、天体Eによる重力、天体Mによる重力、および、天体Eと天体Mの公転速度で回る回転座標系に生じる遠心力、これらの3つの力が釣り合っている。

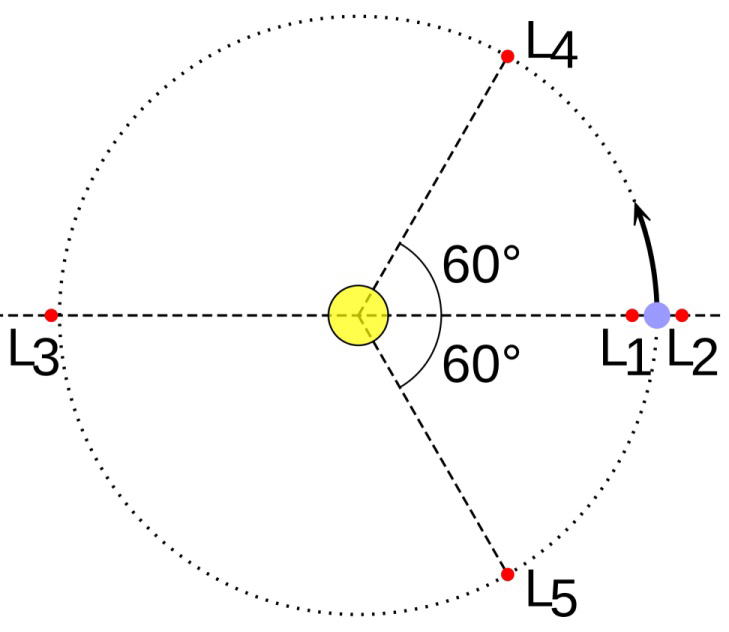
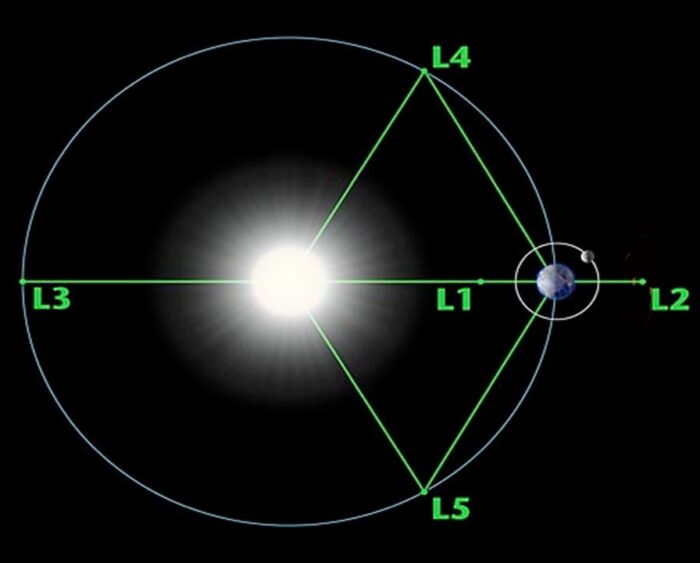
ラグランジュ点は全部で5つあることが知られており、上記の仮定の通り、いずれも天体Eと天体Mの軌道を含む平面内にある。それぞれ L₁からL₅までの番号がふられている。 L₁, L₂, L₃の三点は天体Eと天体Mを結ぶ直線上にある（直線解）。L₄とL₅は天体Eと天体Mを結ぶ線分を一辺とする二つの正三角形の各頂点である（天体Eから天体Mをみたとき、L₄とL₅はそれぞれ60度左右にある）。L₄とL₅の2つの点は特にトロヤ点 (trojan points) と呼ばれる。トロヤ点に天体群が存在するとき、これをトロヤ群とも呼ぶ。上記の仮定に沿うかぎり、ラグランジュ点はあらゆる二天体系に存在し得る。

以上のオイラーとラグランジュの成果は運動方程式を解くことで理論的に得られたものであり、この業績に対してラグランジュとオイラーは1772年のフランス科学アカデミー賞を共同受賞した。後年の発見においては、実際に各種の天体系のラグランジュ点において、小さな天体（天体群）が留まっている実例が確認されている。

ラグランジュ点はスペースコロニー等を建設する際の候補位置でもある。たとえばジェラルド・オニールは、コロニーを地球と月のラグランジュ点に造ることでコロニーの軌道を安定させるアイデアを述べている。

力学的背景

天体Eと天体Mがそれぞれ大きな質量${\displaystyle M_{E}}$と${\displaystyle M_{M}}$をもっており、この二つの天体が円軌道で周回しているとき、この公転周期で回転する回転座標系を考える（回転座標系で天体Eと天体Mは静止している）。${\displaystyle M_{E}}$と${\displaystyle M_{M}}$に比べて無視できるほど小さな質量${\displaystyle m_{A}}$をもつ第三の天体Aについて、いかなる力も受けず、天体Eと天体Mとの相対位置を変えずに留まれる可能性があるラグランジュ点は、次のように捉えられる。天体Aの運動について、初等の古典力学における運動方程式は次のように書ける。

${\displaystyle m_{A}{d^{2}{\boldsymbol {r}}_{A} \over dt^{2}}=\sum _{i}{\boldsymbol {F}}_{i}}$

${\displaystyle {\boldsymbol {r}}_{A}}$は天体Aの位置座標であり、tは時間である。ここでの${\displaystyle {\boldsymbol {F}}_{i}}$は天体Aが受けるそれぞれの力であり、運動方程式ではそれらの総和(合力)を取っている形となる。この形式にて、天体Aが天体Eと天体Mの重力を受ける場合には、運動方程式は次のようになる。

${\displaystyle m_{A}{d^{2}{\boldsymbol {r}}_{A} \over dt^{2}}={\boldsymbol {F}}_{GE}({\boldsymbol {r}}_{E},{\boldsymbol {r}}_{A}) {\boldsymbol {F}}_{GM}({\boldsymbol {r}}_{M},{\boldsymbol {r}}_{A})}$

上記の式ではまだ、回転していない座標系をとっている。${\displaystyle {\boldsymbol {F}}_{GE}({\boldsymbol {r}}_{E},{\boldsymbol {r}}_{A})}$と${\displaystyle {\boldsymbol {F}}_{GM}({\boldsymbol {r}}_{M},{\boldsymbol {r}}_{A})}$はそれぞれ天体Eと天体Mからの重力であり、括弧()内の引数${\displaystyle {\boldsymbol {r}}_{E}}$、${\displaystyle {\boldsymbol {r}}_{M}}$、${\displaystyle {\boldsymbol {r}}_{A}}$は対応する添字の天体の位置座標であり、各重力がこれらの座標変数に依存することを表す。この回転していない座標系の式では、重力を支配する変数が多く、このままでは解析しづらい。そこで、この運動方程式における座標系を天体Eと天体Mの公転に同期して回転する座標系に変換すると、運動方程式は次のようになる。

${\displaystyle m_{A}{d^{2}{\boldsymbol {r}}_{A}' \over dt^{2}}=F_{GE}'({\boldsymbol {r}}_{A}') {\boldsymbol {F}}_{GM}'({\boldsymbol {r}}_{A}') {\boldsymbol {F}}_{w}({\boldsymbol {r}}_{A}') {\boldsymbol {F}}_{v}({d{\boldsymbol {r}}_{A}' \over dt})}$

ここでは、座標変換による変化を受けた物理量には ' (プライム記号)を付した。回転座標系において天体Eと天体Aは静止しているため、これらの座標はそれぞれの重力${\displaystyle {\boldsymbol {F}}_{GE}'({\boldsymbol {r}}_{A}')}$と${\displaystyle {\boldsymbol {F}}_{GM}'({\boldsymbol {r}}_{A}')}$において定数として扱うことができ、各重力値を変化させる変数は天体Aの座標${\displaystyle {\boldsymbol {r}}_{A}'}$のみとなる。こうして、重力を比較的簡単に評価できるようになった。一方で、この回転座標系へと変換したことで、遠心力である${\displaystyle {\boldsymbol {F}}_{w}({\boldsymbol {r}}_{A}')}$とコリオリの力である${\displaystyle {\boldsymbol {F}}_{v}({d{\boldsymbol {r}}_{A}' \over dt})}$が新たに追加されることになるが、これらはさしあたって問題にはならない。${\displaystyle {\boldsymbol {F}}_{w}({\boldsymbol {r}}_{A}')}$の変化は天体Aの位置${\displaystyle {\boldsymbol {r}}_{A}'}$のみに依存しており、その解析は比較的容易である。また、ラグランジュ点において天体Aが静止している場合だけを当面問題にするならば、天体Aの速度${\displaystyle {d{\boldsymbol {r}}_{A}' \over dt}}$はゼロであり、これに起因するコリオリの力${\displaystyle {\boldsymbol {F}}_{v}({d{\boldsymbol {r}}_{A}' \over dt})}$の項はゼロとして扱える。当然ながら、ラグランジュ点では天体Aは加速を受けないから、左辺のなかの天体Aの加速度${\displaystyle {d^{2}{\boldsymbol {r}}_{A}' \over dt^{2}}}$もゼロである。したがって、ラグランジュ点を解析的に求める問題は、${\displaystyle {\boldsymbol {r}}_{A}'}$だけが変数となる次の方程式の解を求めることに帰着できる。

${\displaystyle 0={\boldsymbol {F}}_{GE}({\boldsymbol {r}}_{A}) {\boldsymbol {F}}_{GM}({\boldsymbol {r}}_{A}) {\boldsymbol {F}}_{w}({\boldsymbol {r}}_{A})}$

以上の方程式の解の意味するところは、概要で述べた通り「回転座標系の天体Aについて解の位置${\displaystyle r_{A}}$では、Eの重力、Mの重力および遠心力の3つの力が釣り合う（ゼロとなる）」ということに他ならない。ここで、以下のそれぞれの条件を満たすポテンシャル${\displaystyle U_{GE}({\boldsymbol {r}}_{A})}$、${\displaystyle U_{GM}({\boldsymbol {r}}_{A})}$、${\displaystyle U_{w}({\boldsymbol {r}}_{A})}$を考える。

${\displaystyle {\boldsymbol {F}}_{GE}({\boldsymbol {r}}_{A})=-\nabla U_{GE}({\boldsymbol {r}}_{A})}$

${\displaystyle {\boldsymbol {F}}_{GM}({\boldsymbol {r}}_{A})=-\nabla U_{GM}({\boldsymbol {r}}_{A})}$

${\displaystyle {\boldsymbol {F}}_{w}({\boldsymbol {r}}_{A})=-\nabla U_{w}({\boldsymbol {r}}_{A})}$

これらのポテンシャルを用いて運動方程式を再度書き直すと、次のようになる。

${\displaystyle 0=-\nabla \{U_{GE}({\boldsymbol {r}}_{A}) U_{GM}({\boldsymbol {r}}_{A}) U_{w}({\boldsymbol {r}}_{A})\}}$

これまでの方程式では、それぞれの力${\displaystyle {\boldsymbol {F}}({\boldsymbol {r}}_{A})}$は3成分のベクトル量であったが、ポテンシャル${\displaystyle U({\boldsymbol {r}}_{A})}$は1成分のスカラーである。そのため、ラグランジュ点を求めるにあたっては、次のポテンシャル${\displaystyle U_{total}({\boldsymbol {r}}_{A})}$で考えることで、直観的なイメージがしやすい。

${\displaystyle U_{total}({\boldsymbol {r}}_{A})=U_{GE}({\boldsymbol {r}}_{A}) U_{GM}({\boldsymbol {r}}_{A}) U_{w}({\boldsymbol {r}}_{A})}$

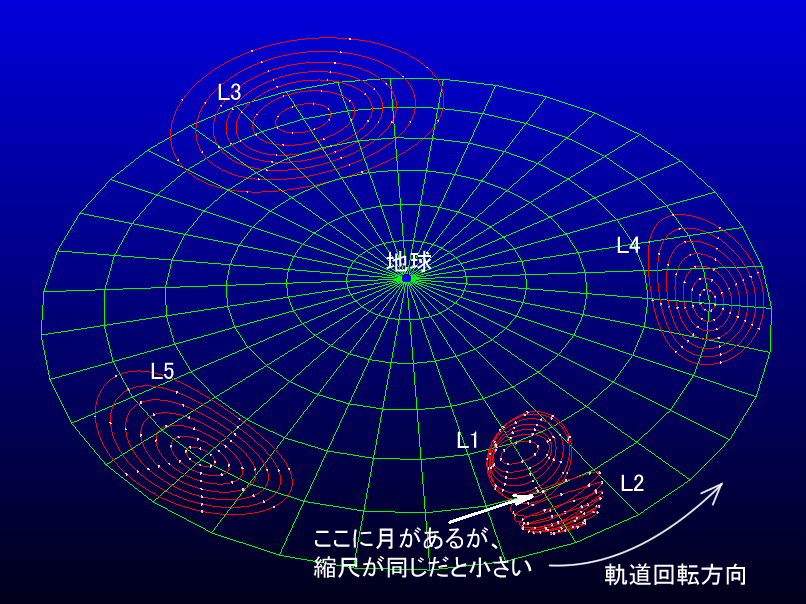
たとえば、天体Eと天体Mの公転軌道を含む平面上の${\displaystyle U_{total}({\boldsymbol {r}}_{A})}$について、この平面上にできた回転座標系中のポテンシャルエネルギー (ロッシュ・ポテンシャル)の高低を三次元グラフで図示することができる。ポテンシャルエネルギーを表す曲面において、各位置にある物体は曲面のより低い方向へ力を受けると理解することができる。ラグランジュ点を求めるということは、ロッシュ・ポテンシャルの曲面において、平坦な場所（勾配ゼロ、すなわち、力を受けない場所）を探すことに相当する。なお、ロッシュ・ポテンシャルの形状を定めるパラメーターは、（縮尺を除いて）天体Eと天体Mの質量比${\displaystyle M_{E}/M_{M}}$のみであることが知られている。

以上の式を解析して求められたラグランジュ点は5つ存在し、それらはL₁からL₅まで番号が付けられ（冒頭図も参照）、それぞれ下記の各節のように定義されている。以下では、この方程式の天体Eと天体Mの系における各ラグランジュ点について述べる。

直線解

5つのラグランジュ点のうちL₁, L₂, L₃はオイラーの直線解と呼ばれ、いずれも、天体Eと天体Mを結ぶ直線上にある。

L₁

L₁は天体Eと天体Mの2物体を結ぶ直線上にあり、天体Eと天体Mの間に存在するラグランジュ点である。一般に、地球よりも太陽に近い軌道を回る物体は、地球よりも短い公転周期を持つ。しかし、これは地球の重力による影響を考慮すると、物体が太陽に引かれる力は弱められ、その物体の公転周期は長くなる。もしその物体の位置がL₁に一致するならば、上記の効果によって、その物体の公転周期は地球の公転周期とちょうど等しくなる。

太陽-地球系のL₁は、太陽と地球の間において月の公転軌道より外側で、太陽の観測を行うのに理想的な場所のひとつである。地球からは約150万kmの距離で、金星の公転軌道からは約4,000万km離れている。太陽・太陽圏観測機 (SOHO) は、L₁の付近のハロー軌道を周回している。地球-月系のL₁は、ここを経由することで最小限の軌道変更で月や地球をそれぞれ周回する軌道へと入ることができる。このため、荷物や人員を地球と月の間で行き来させるための中間有人宇宙ステーションの場所として理想的とされる。

L₂

L₂ は天体Eと天体Mの2物体を結ぶ直線上にあり、天体Eと天体Mのうち質量の小さい天体の外側に位置するラグランジュ点である。太陽からみて地球より遠くにある物体は、通常は地球よりも長い公転周期を持つ。しかし、その物体が太陽から見て地球の裏側にある場合には、地球の重力の影響が加わり、これを考慮すると、その物体の公転周期は短くなる。もし太陽-地球系のL₂にその物体があれば、この効果によって公転周期が地球と等しくなる。太陽-地球系のL₂は地球から約150万km（1/100天文単位）の位置にある。

太陽-地球系のL₂は、地球によって太陽からの放射物が遮られているために、宇宙空間での観測を行うのに適した場所である。L₂付近にある物体には太陽光が遮光されており、得られた観測結果の較正を行いやすい。到達は比較的困難であり、例としてジェイムズ・ウェッブ宇宙望遠鏡（JWST）は発射から到達まで30日を要した。有人探査機ではまだ到達していない。

地球-月系のL₂は、月から61,500kmの位置にあり、月の裏側をカバーする通信衛星の位置として都合が良いとされる。

天体Mの質量${\displaystyle M_{M}}$が天体Eの質量${\displaystyle M_{E}}$に比べて非常に小さい場合には、L₁とL₂は天体Mからほぼ等しい距離(以下の式のr)の位置になる。これはヒル圏 (Hill sphere) の半径に等しく、Rを天体Eと天体Mの距離として以下の式で表される。

${\displaystyle r\approx R{\sqrt[{3}]{\frac {M_{M}}{3M_{E}}}}}$

この半径rの円軌道で天体Mの周囲を回る物体の軌道周期は、天体Mが天体Eの周囲を回る公転周期の0.58倍となる。

L₃

L₃ は天体Eと天体Mの2物体を結ぶ直線上にあり、天体Eと天体Mのうち質量の大きい天体の外側に位置するラグランジュ点である。

太陽-地球系のL₃は、地球から見て太陽の裏側で、地球の公転軌道の外側にある。 また、太陽からL₃までの距離は太陽から地球までの距離よりも短い。 これらの配置は、太陽と地球が重心を共通の中心として回転しているために生じる。

一般に、地球の公転軌道の外側を回転する物体は地球より長い公転周期を持つ。 しかし、地球の重力による影響を考慮すると、その物体が太陽の方向に引かれる力は強められ、その物体の公転周期はより短くなる。 このため、L₃ではその物体の公転周期は地球と等しくなる。

L₃は地球からの通信が太陽によって遮られる、L₃で観測をするメリットがほとんど無い、到達が比較的困難であるため観測機が設置されたことはない。

三角解（トロヤ点）

L₄ と L₅ は、正三角形解またはトロヤ点などとも呼ばれるラグランジュ点である。天体Eと天体Mを結ぶ線分を一辺とする正三角形の3番目の各頂点の位置にある。天体Mが天体Eの周りを公転する軌道上で、天体Mに先行あるいは追従する相対位置にある。仮定の通り、公転の中心は天体Eと天体M系の重心にある。回転しない座標系からみると三角解点では、天体Eの重力と天体Mの重力の合力が、ちょうど両者の重心への向心力として働いている。三角解点の軌道長半径は天体Eと天体Mの間の距離よりわずかに短く、天体Mの軌道長半径よりわずかに長い。

仮に天体Eの質量が天体Mより大きいとすると、それらの質量比${\displaystyle M_{E}/M_{M}}$が24.96倍以上ならば、L₄とL₅は安定な均衡点となることが分かっている。

太陽-地球系のL₄とL₅は、地球が太陽を回る公転軌道上において、地球より60度先行した位置にL₄が、同じく60度後ろの位置にL₅がある。L₄とL₅は、後述するように摂動に対して安定な平衡点であるため、1969年にジェラルド・オニールの提案したスペースコロニーの設置場所候補として採用されている。

安定性

各ラグランジュ点について、まず狭義の安定性（平衡解の位置に静止した状態を継続し続けるかどうか）について述べる。オイラーの直線解（L₁, L₂, L₃）において天体Aは、天体Eと天体Mを通る直線の垂直方向にはラグランジュ点に引き戻す力を受ける。一方、同直線方向にはラグランジュ点から引き離す力を受ける。トロヤ点（L₄, L₅）では、各ラグランジュ点からどの方向にわずかに動いても、元の位置から遠ざかる方向に力を受ける。このように、静止位置から摂動を受けた際にラグランジュ点から遠ざかる方向へ力を受け得るという意味では、すべてのラグランジュ点（L₁からL₅）は狭義には安定ではない。

以下では、同じく各ラグランジュ点について、より広義の安定性（すなわち、平衡解位置の付近で定常的な往復・振動運動（閉じた軌道運動）をすることで、平衡解の近くに長期間滞在できるかどうか）について述べる。

この意味での安定性について、L₁, L₂, L₃ は少なくとも制限三体問題において、各点の近くに安定な周期軌道が存在することが分かっている。これらは完全な周期軌道であり、ハロー軌道と呼ばれる。

同じくこの意味での安定性についてL₄とL₅は、2天体(EとM)の質量比が${\displaystyle M_{E}/M_{M}>24.96}$ を満たす場合において、各ラグランジュ点の付近で安定に閉じた軌道運動ができる。太陽-地球系や地球-月系などにおいて、上記の質量比の条件が満たされている。L₄やL₅において、ある物体が適切な速度を有していると、回転座標上のポテンシャルのなかでコリオリの力を受けながら軌道運動を行い、L₄やL₅の周囲を周回する。この軌道は、回転座標系における等ポテンシャル線に沿ったインゲン豆型の安定な軌道である。

また、太陽系のような制限なしの多体力学系にはL₁, L₂, L₃にあるようなハロー軌道は存在しないが、準周期的なリサジュー軌道が存在する。リサジュー軌道は完全に安定ではないが、比較的小さな労力で長期にわたって、目的の位置（リサジュー軌道上）に宇宙機を留めておくことができる。リサジュー軌道は、これまで行われた（ラグランジュ点を利用するものを含めた）全ての宇宙ミッションで実際に使われてきた。少なくとも太陽‐地球系のL₁を使うミッションでは、L₁付近に宇宙機を置くよりも、大きな振幅 (100,000 – 200,000 km) を持つリサジュー軌道に置いた方が運用上好都合なことがある。たとえば、リサジュー軌道で宇宙機を太陽と地球を結ぶ直線から外れた位置に滞在させることで、地球と宇宙機間の通信への太陽の干渉が低減するメリットがある。

例

太陽-木星の系では、トロヤ群と呼ばれる数千個の小惑星が本系のL₄, L₅に付近に軌道を持っており、L₄のものを「前トロヤ小惑星群」、L₅のものを「後トロヤ小惑星群」とそれぞれ呼んでいる。このような小さな天体群は、恒星-惑星系（先述の木星の他に、太陽-土星系や太陽‐火星系など）だけでなく惑星-衛星系（木星とその衛星の系、土星とその衛星の系など）にも発見されている。

土星とその第3衛星テティスの系のL₄とL₅には、それぞれ2つの小さな衛星（第13衛星テレスト(L₄付近)と第14衛星カリプソ(L₅付近)）が確認されている。また、土星-第4衛星ディオネの系でも、ヘレネ（第12衛星; L₄付近）とポリデウケス（第34衛星; L₅付近）が存在する。このような惑星-衛星の系のL₄とL₅に位置する衛星はトロヤ衛星と呼ばれ、それぞれのL₄とL₅の等ポテンシャル線上を周回している。軌道の周回に伴う方位角の変化は、ポリデウケスが最も大きく、土星-ディオネ系のL₅の方向から最大で32度離れる。なお、テティスもディオネも、これらのトロヤ衛星群と比べてずっと質量が大きい。さらに、土星はテティスやディオネよりもずっと大きな質量をもつ。このために、木星を取り巻くそれぞれの恒星-惑星系および惑星-衛星系のそれぞれのラグランジュ点は、十分に安定した軌道を有している。

太陽‐地球系のトロヤ点には大きな天体は見つかっていないが、星間塵がL₄とL₅を取り巻くように分布していることが1950年代に発見されている。また、対日照よりもずっと淡いとされる塵の雲（コーディレフスキー雲）が地球-月系のL₄, L₅に存在するとする説もある。

他の同期軌道天体

地球の同期軌道天体である小惑星クルースンは、見方によって異なる捉え方のできる小惑星である。太陽-地球系の回転座標系からクルースンをみると、トロヤ群天体のように、太陽-地球系のラグランジュ点L₄の周囲の等ポテンシャル線上を周回するインゲン豆型軌道に似た運動をしている。

一方で、静止した座標系からクルースンをみると、別の解釈もできる。クルースンは太陽を周回する軌道上を運動しているが、クルースンは地球との相対位置によって地球の重力を受けて速度を変える。この結果として、クルースンは太陽との距離（軌道半径）を連続的に大小させる。このように、静止座標系での地球の影響をうけて軌道半径を変えるサイクルを繰り返している、と理解することも可能である。なお、地球とクルースンの運動エネルギーのやり取りにおいては、地球の公転周期（つまり1年の長さ）はほとんど影響を受けない。これは、クルースンの質量が地球の質量と比べて1/200億と十分に小さいためである。

土星の第10衛星ヤヌスと第11衛星エピメテウスも上記と似た関係にあるが、ヤヌスはエピメテウスよりやや質量が大きいのみなので、ヤヌスの側も無視できないほどの軌道の変化を受ける。ラグランジュ点を考えるに際して、第三の天体Aが天体Eや天体Mと比べて無視できるほど小さな質量をもつことを前提としたが、天体A（ここではエピメテウス）と天体M（ここではヤヌス）とではこの質量比の要請を満たしていないことが理由である。

また、類似の別の現象として軌道共鳴がある。軌道運動をしている天体同士がある共鳴条件（両者の公転周期が単純な整数比となる等）を満たすと、相互作用が強くはたらき、両天体の公転運動が相関性を示す（共鳴現象）。

宇宙地政学的重要性

地球の表面（リソスフェア、水圏、大気圏）において、地峡や海峡などの地理的な特徴を有する重要地点の政治支配・軍事支配が地政学上の検討対象となっているが、これを拡張した同様の検討が地球周辺の宇宙空間の「支配」についてもなされている。エヴェレット・C・ドールマンの『宇宙時代の地政戦略---アストロポリティックスによる分析』では、ラグランジュ点について論及されている。地球や宇宙の特定の場所の「支配」によって、効率性の面からかなり有利な立場を得ることができ、交易面でも軍事面でも重要と指摘されている。2018年5月に中国が世界初のラグランジュ点を周回する通信衛星鵲橋を打ち上げ、さらに、2019年1月3日に同国が嫦娥4号による人類史上初の月の裏への着陸に成功した際には、地政学的・軍事的な狙いを懸念する声もあがるなど、ラグランジュ点は宇宙地政学的な重要性が指摘されつつある。

脚注

注釈

出典

参考文献

• 堀源一郎『天体力学講義』東京大学出版会、1988年。ISBN 978-4130621182。 
• コリン・グレイ、ジェフリー・スローン編、奥山真司訳・解説『進化する地政学 - 陸、海、空そして宇宙へ』五月書房〈戦略と地政学 1〉、2009年。ISBN 978-4-7727-0479-3。 

関連項目

• ラグランジュ点に存在する物体の一覧
• トロヤ群
• 地球のトロヤ群
• トロヤ衛星
• スペースコロニー
• 小惑星帯
• 機動戦士ガンダム

外部リンク

• NASAのWMAPのサイトにあるラグランジュ点の説明。L4, L5 が安定になる条件の導出など （英語）
• カリフォルニア大学リバーサイド校の John Baez 教授によるラグランジュ点の説明 （英語）