擬絶対値

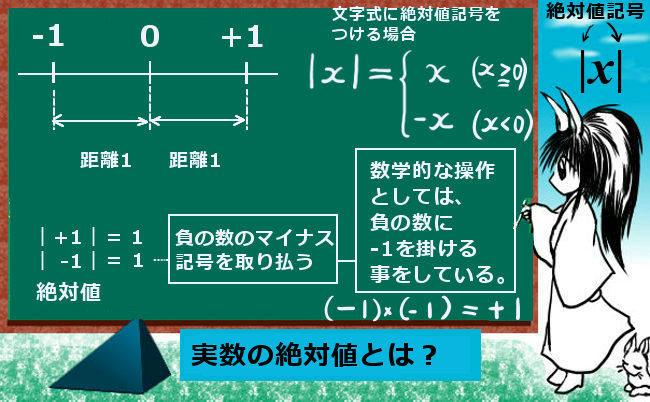
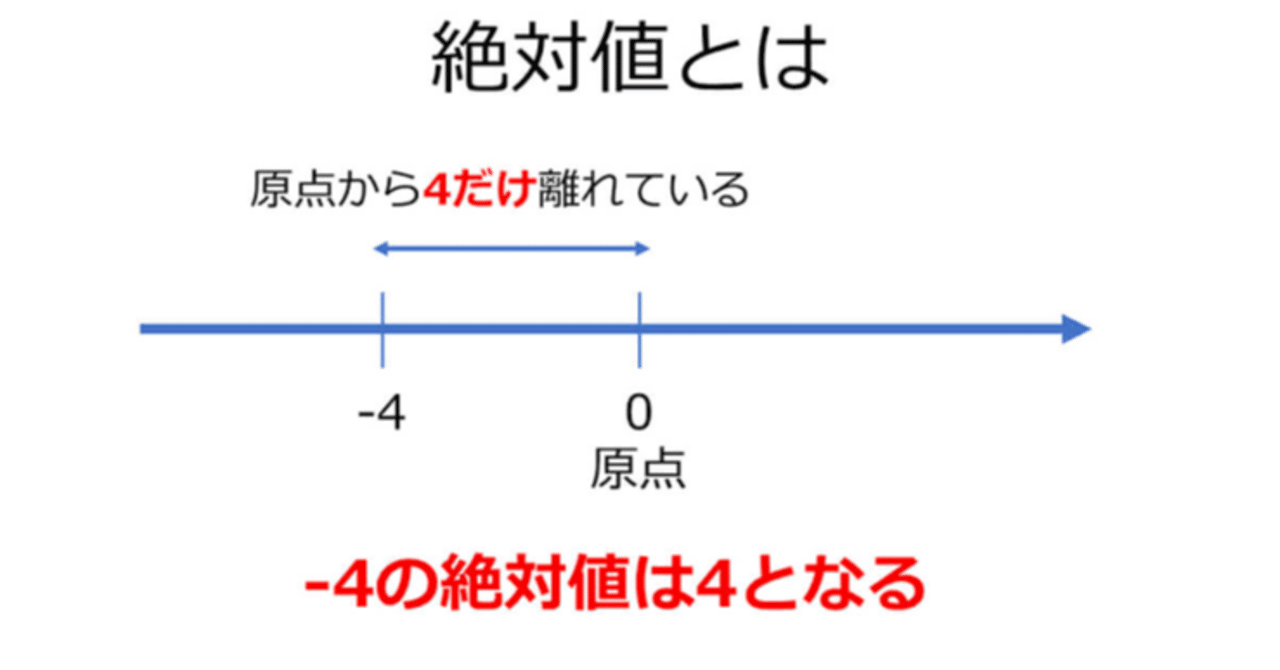
数学における擬絶対値（ぎぜったいち、英: pseudo-absolute value, 独: Pseudobetrag）は、絶対値よりも条件の緩い類似の概念である。

定義

R を単位的環とする。非負実数値函数 |•|: R → R が擬絶対値であるとは、以下の三条件をすべて満たすときにいう: a, b ∈ R を任意として

1. 定値性: ${\displaystyle |a|=0\iff a=0,}$
2. ${\displaystyle |a-b|\leq |a| |b|,}$
3. 劣乗法性: ${\displaystyle |a\cdot b|\leq |a|\cdot |b|.}$

条件 3 の代わりにより強く

3a. 乗法性: ${\displaystyle |a\cdot b|=|a|\cdot |b|}$

を満たすものは絶対値と言う。

擬絶対値 |•| が非アルキメデス的とは

${\displaystyle |a b|\leq \max(|a|,|b|)}$

を満たすときに言う。

性質

• 擬絶対値は各元 a ∈ R に対して必ず |−a| = |a| を満たす。また、各元 a, b ∈ R に対して三角不等式 |a b| ≤ |a| |b| を満たす。
• 擬絶対値に関して必ず |1| ≥ 1 が成り立ち、特に絶対値に関して |1| = 1 が成り立つ。
• 絶対値を持つ任意の単位的環は整域でなければならない（乗法性により、実数の零積性質がその環に遺伝する）。

例

以下 (R, |•|) は擬絶対値持つ単位的環とする。

多項式環の擬絶対値

多項式環 R[X] または多変数の R[X₁, …, X_n] はそれ自体（多項式の積に関して）単位的環を成す。ここでたとえば、1-擬ノルムは多項式環上の擬絶対値を与える。

行列環の擬絶対値

同様に行列環 R^n×n も（行列の積に関して）単位的環を成し、ここでも 1 ≤ p ≤ 2 なる各実数 p に対する p-擬ノルムが行列環上の擬絶対値を与える。

注

注釈

出典

参考文献

関連項目

外部リンク